About the Algebra (Main) App
Covered Topics
Algebra through Pre-Calculus, including topics well beyond those included in the Algebra Handbook. Specifically, the app covers linear, absolute value, quadratic, cubic, polynomial, exponential, logarithmic, rational and hyperbolic functions, as well as systems of equations and inequalities, exponents and logarithms, conic sections, polar coordinates, complex numbers, the Binomial Theorem, Pascal's Triangle, famous curves, and important mathematical constants. Upon completion, the app will also cover vectors, general functions, composite functions, radical functions, the Gamma Function and Riemann Zeta Functions.
Values (coefficients, constants, etc.) may be entered as integers, fractions, mixed numbers or decimals. Many of the modules allow solutions to be expressed as fractions or decimals, according to the user's choice.
The app also contains an extensive glossary of terms relating to Algebra (up to and including Pre-Calculus).
To download the app now, click here: Download the Algebra (Main) App version 0.8c.
Samples of What the App Can Do
Quick links to sample categories:
| Quadratic Functions | Rational Functions | |
| Systems of Equations | Exponents and Logarithms | |
| Polynomials | Conic Sections | |
| Polar Coordinates | Complex Numbers |
Quadratic Functions
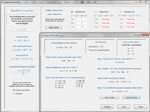
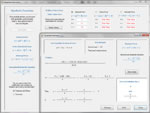
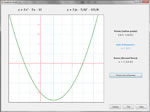
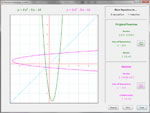
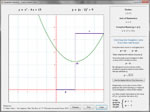
Define a quadratic function in either General Form, Vertex Form or Intercept Form. Then, factor the function, set it equal to zero and solve it, complete the square, use the quadratic formula, graph the function directly or via transformation, develop its inverse, or convert it to another form. Below are some thumbnails that you can click to get a better idea of what you can do with Quadratic Functions. Note: one of the more interesting things you can do, which is rarely taught in schools, is to find the complex roots of a quadratic function based on its graph (see Thumbnail "Complex Roots" below).
 |
 |
 |
 |
 |
|---|---|---|---|---|
| Factoring | Quadratic Formula | Graph | Inverse | Complex Roots |
Systems of Equations
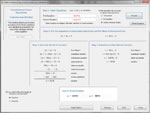
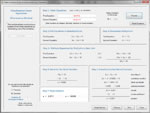
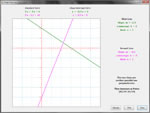
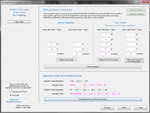
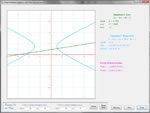
Solve a system of two linear equations using substitution, elimination, or graphing; the app will do all three. If solving by substitution, the app puts one of the equations in slope intercept form before substituting - you may choose which equation to put in this form or let the computer decide. If solving by elimination, you may choose which variable to eliminate; see what happens when you solve the equation once by eliminating x and once by eliminating y. Solve a system of equations in which one equation is linear and one is conic. Define the conic equation in general or standard form. Below are some thumbnails that you can click to get a better idea of what you can do with Systems of Equations.
 |
 |
 |
 |
 |
|---|---|---|---|---|
| Solve by Substitution |
Solve by Elimination |
Solve by Graphing |
Define a Line and a Conic Section |
Find the Intersection of a Line and a Conic |
Polynomials
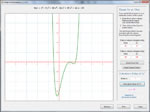
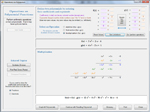
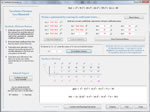
Define a polynomial directly or defined based on its roots. Factor it, graph it and solve it. If you want to save a polynomial for later, copy it to the internal clipboard so it can be recalled elsewhere in the app, including as part of a rational function. On the graphing page, enter a value of x and obtain the corresponding value of y. Add, subtract and multiply polynomials, or perform synthetic division by either a binomial or a trinomial. Below are some thumbnails that you can click to get a better idea of what you can do with Polynomials.
 |
 |
 |
 |
 |
|---|---|---|---|---|
| Define a Polynomial |
Factor and Find Real Zeros |
Graph the Polynomial |
Multiply Two Polynomials |
Synthetic Division by a Binomial |
Polar Coordinates
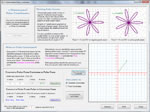
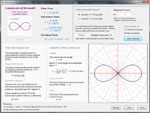
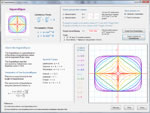
Define polar and rectangular coordinates in 2D, and convert points between systems. In 3D, define rectangular, cylindrical and spherical coordinates, and convert among systems. Investigate parametric equations. Check out over a dozen two-dimensional functions that are defined in terms of polar coodinates. Examples include the cardioid, the lemniscate, the cycloid, the catenary and the superellipse. Below are some thumbnails that you can click to get a better idea of what you can do with Polar Coordinates.
 |
 |
 |
 |
 |
|---|---|---|---|---|
| Conversion between 2D Systems |
Conversion among |
Parametric Equations |
Lemniscate of Bernoulli |
Family of Superellipses |
Rational Functions
Simple Rational functions can be defined in standard form or binomial form. General rational functions can be defined by entering the numerator and denominator coefficients or by pasting coefficients from the clipboard. It is also possible to define the polynomials in the numerator and denominator using the roots of the polynomials, both real and complex. Once entered, you can find asymptotes, holes and intercepts, and graph the function. Below are some thumbnails that you can click to get a better idea of what you can do with Rational Functions.
 |
 |
 |
 |
 |
|---|---|---|---|---|
| Simple Rational Function |
General
Rational |
Define General Function from Roots |
Factor a General Rational Function |
Graph a General Rational Function |
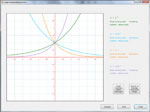
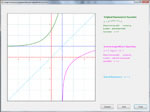
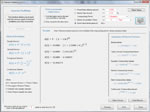
Exponents and Logarithms
Define and graph one or more exponential or logarithmic functions. Solve exponential andlogarithmic equations. Examine the behavior of multiple functions around the origin. Develop inverse functions step-by-step. Solve interest problems for any of the variables involved in the computation, and see comparisons of accumulated interest over time under varying compounding methods. Even get a little history on why logarithms exist. Below are some thumbnails that you can click to get a better idea of what you can do with Exponents and Logarithms.
 |
 |
 |
 |
 |
|---|---|---|---|---|
| Exponential Equation |
Multiple Functions on One Graph |
Inverse Function | Interest Problem | History of Logarithms |
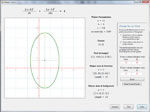
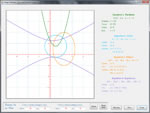
Conic Sections
Compare the equations, parameters and characteristics of the various conic section curves. Define a curve using either standard form or general form. Identify a curve entered in standard form and convert it to standard form. Graph one or more curves on a single set of axes. Below are some thumbnails that you can click to get a better idea of what you can do with Conic Sections.
 |
 |
 |
 |
 |
|---|---|---|---|---|
| Comparison of Conic Section Curves |
Standard Form |
Graph a
Conic Section Curve |
Identify and
Convert to Standard Form |
Graph Multiple Curves |
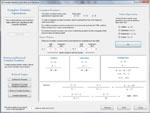
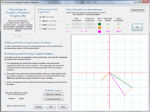
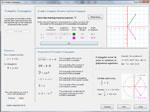
Complex Numbers
Define and perform arithmetic operations on complex numbers, either algebraically or graphically. Investigate complex conjugates. Find n-th roots of 1. What is the square root of i. Can I use complex numbers to prove that 1 = -1? What is DeMoivre's Theorem? Can I take a complex number to a complex exponent? Below are some thumbnails that you can click to get a better idea of what you can do with Complex Numbers.
 |
 |
 |
 |
 |
|---|---|---|---|---|
Algebraic |
Graphical |
Conjugates | DeMoivre's Theorem |
Complex Exponents |
To download the app now, click here: Download the Algebra (Main) App version 0.8c.